Komplexe Früchte

Rike und Ben sind im Supermarkt und wollen Obst kaufen. Sie überlegen, ob die Früchte auch so gut schmecken, wie sie aussehen.

Rike Da fällt mir die Cauchy-Integralformel ein. Damit kann man mit dem Integral über die Oberfläche die Funktionswerte mittendrin ausrechnen.

Ben Das kommt mir komisch vor. Hatten wir nicht vor kurzem noch das Residuum für Funktionen mit Singularitäten?

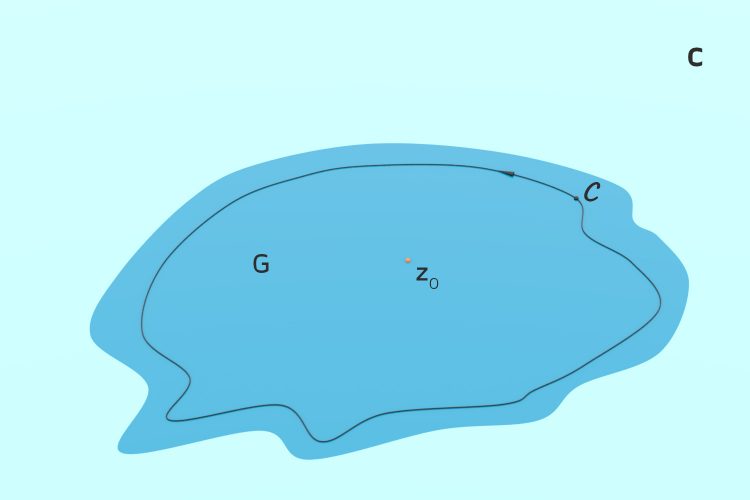
Rike Richtig. Die Voraussetzung für diese Integralformel ist, dass die Funktion f in einem beschränkten, einfach zusammenhängenden Gebiet G, 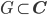differenzierbar ist.

Residuensatz

Ben Na gut, die Funktionen mit Singularitäten sind nicht differenzierbar, Du hattest

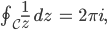
stimmts?
Rike Richtig. Aus dieser Tatsache kannst Du die Integralformel herleiten.

Herleitung der Integralformel

Du nimmst einen Punkt z₀ aus G. Dann ist die Funktion

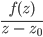
in 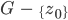stetig differenzierbar, Du legst eine glatte Kurve 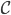um z₀

und berechnest das Integral

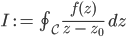
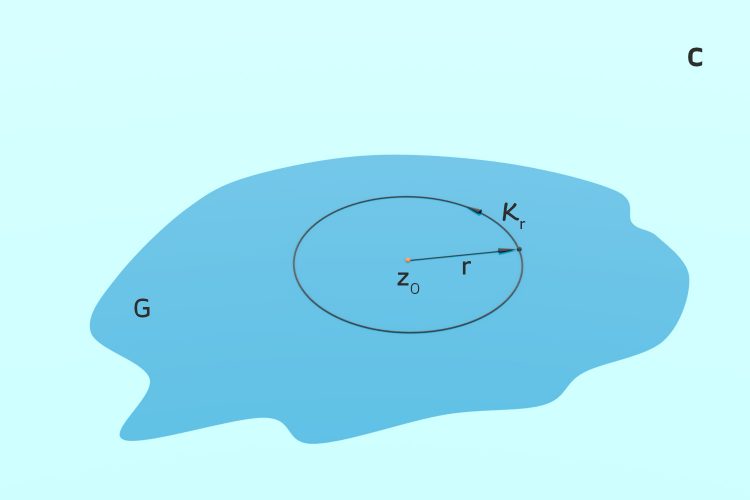
Das Integral ist nicht von der Kurve selbst abhängig, genauso könntest Du einen Kreis 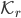mit einem festen Radius r wählen, sodass 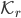vollständig in G liegt.

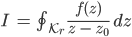
Wenn Du nun den Kreis immer kleiner werden lässt, dann geht f(z) nach f(z₀):

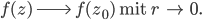
Das Restintegral lautet dann

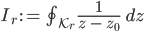
Jetzt nehmen wir eine ähnliche Substitution wie im Urlaub für z:

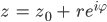
Dann wird

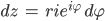
Aus dem Integral I_r wird damit:

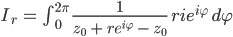
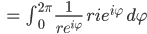
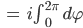
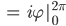
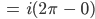
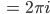
Cauchy-Integralformel

Und weil das Integral unabhängig von der Kurve ist, kriegen wir

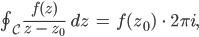
das kannst Du prima umstellen und kriegst die Cauchy-Integralformel:

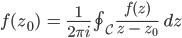
Ben Gut, verstehe. Das ist echt ‘ne tolle Sache, ich integriere über den Rand und kriege die Information im Innern. Gefällt mir! Klappt das auch im R³?

Rike Nö!

Ben Dann lass uns doch mal in den Supermarkt für komplexe Früchte gehen!

Rike Hahaha!

Übungsaufgaben

Überprüfe

1. in
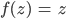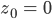
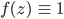2. in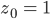

Lösung

1. f(0) = 0
2. f(0) = 1