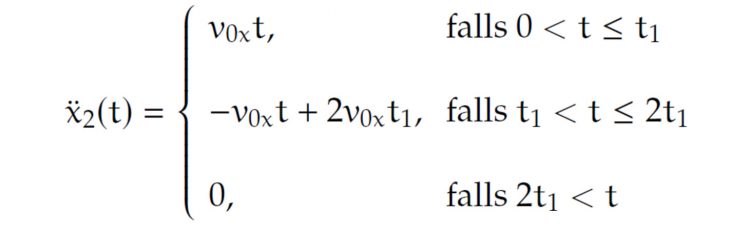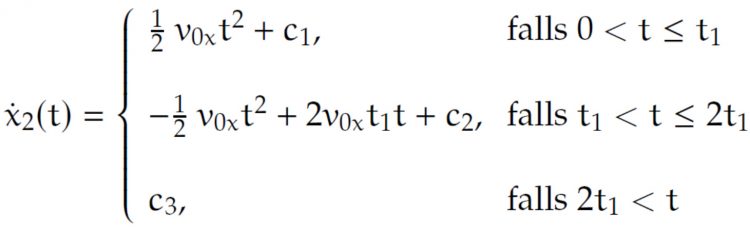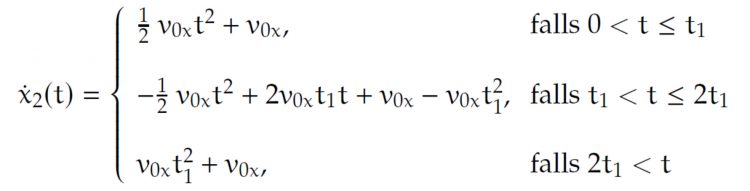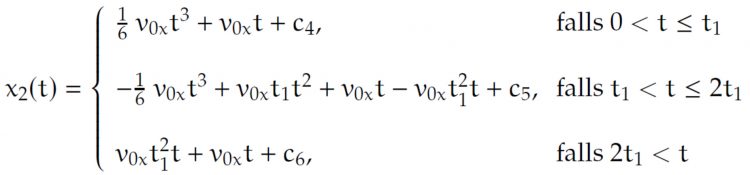Skip to main content


Zutaten: Zucker, Kakaomasse (50%), Milchzucker, Weizenmehl, Vollmilchpulver, Magermilchpulver, Butterreinfett, Sahnepulver, Butter (1,4%)
Kann Spuren von Analysis und Geometrie enthalten.

IV_03_titel_handball

Besser als ein Parabelwurf

Marietta Ehret Analysis, Differenzialgleichungen

Max hat seinen Bachelorabschlussfilm geschnitten und ist mit seinen Handballfreunden aus der Provinz nach Berlin zum WM-Spiel Deutschland gegen Frankreich gefahren. Unglaublich, diese Stimmung in der Halle. Stefan Kretzschmar ist da, Markus Baur ist da. Einige der Nationalspieler hat er natürlich schon bei Bundesligaspielen in Lemgo gesehen, aber die Nationalmannschaft, das ist noch mal was anderes.

Parabelwurf

Er sieht, wie Uwe Gensheimer den Ball so kraftvoll wirft und den zweiten Siebenmeter verwandelt, gibt es da ein Geheimnis? Max kennt ja die vielen  Trainingsmethoden, aber Uwes Wurf ist wirklich genial. Wie kann das sein? Ein normaler Wurf hat eine Richtung, gegeben durch die beiden Komponenten der Anfangsgeschwindigkeit (v0x, v0y). Dann fliegt der Ball eine Parabel:

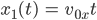
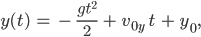
wenn wir mal das x-y-Koordinatensystem so setzen, dass

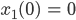
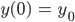
ist. Vielleicht kann Gensheimer dem Ball mit seinem Handgelenk eine Beschleunigung in horizontale Richtung geben?  So eine Art Dirac-Stoß? Das muss es sein! Er fragt seine Freund Patrick um Rat.

Anfangsbeschleunigung

Patrick Das mit dem Dirac-Stoß ist hohe Mathematik, lass mal ruhig angehen. Wir nehmen mal eine Dreiecksfunktion, solange er den Ball in der Hand hält, wird die Beschleunigung immer größer, und dann geht sie wieder auf Null runter.

IV_03_formel_01

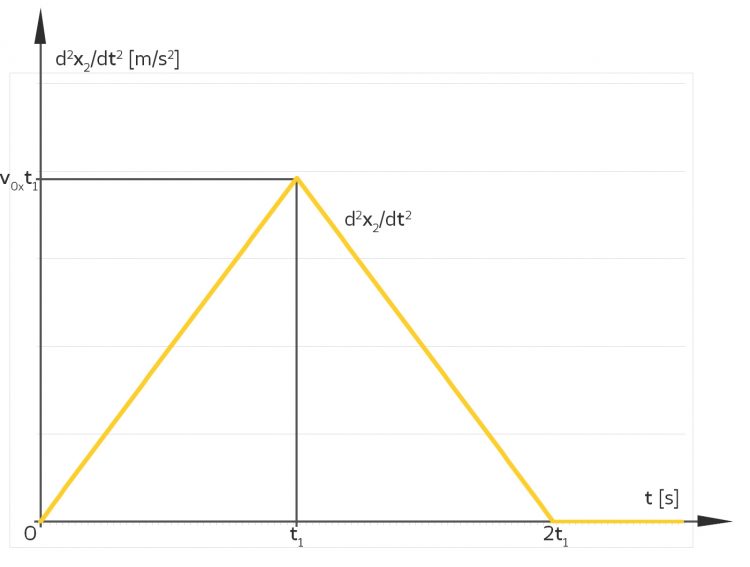
03_2019-kurve-handball_03-05
Anfangsbeschleunigung für den Profiwurf

Max Okay, dann habe ich eine stückweise Funktion für

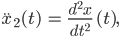
die brauche ich nur noch zu integrieren. Hab ich schon mal gemacht, das kriege ich hin!

Patrick Ja, mach mal!

Integration der stückweisen Funktion

Max Gut, die 2. Ableitung ist dann das Dreieck und für die 1. Ableitung kriege ich durch Integration

Patrick Jetzt mußt Du nur noch den Anfangswert für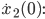

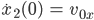
einsetzen und an den Stellen t = t1 und t = t2 für Stetigkeit sorgen.

Max Okay, dann kriege ich

IV_03_formel_03

Und jetzt noch mal integrieren?

Patrick Ja!
Max Na gut, dann kriege ich

IV_03_formel_05

Patrick Jetzt noch mal 'nen Anfangswert

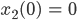
und die Stetigkeit bei t = t1 und t = t2 ergibt die finale Lösung.

Finale Profiwurflösung

Max Gut, dann habe ich

IV_03_formel_04

Lass uns beide Kurven zeichnen, die „normale“ und die „Gensheimer“-Kurve:

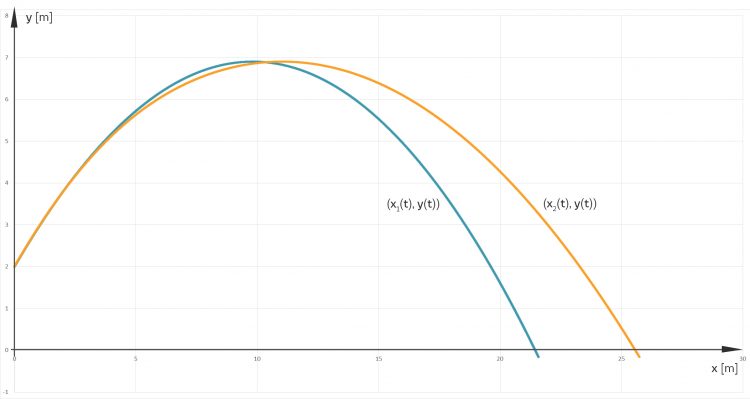
03_2019-kurve-handball_01-03
In Blau die normale Parabel, in Orange die mit der Anfangsbeschleunigung. t1 = 0,5 s; v0x = v0y = 9,81 m/s; y0 = 2 m

Patrick Mit einer echten Beschleunigung kommt Gensheimers Ball viel weiter. So ein Wurf hat viel mehr Power! Kannst Du mal die erste Ableitung der beiden vergleichen?

Max Hier! Die „normale“ Parabel hat in x-Richtung immer die Geschwindigkeit v10x, aber der Gensheimer-Wurf wird viel schneller. Das ist es, Patrick, super!

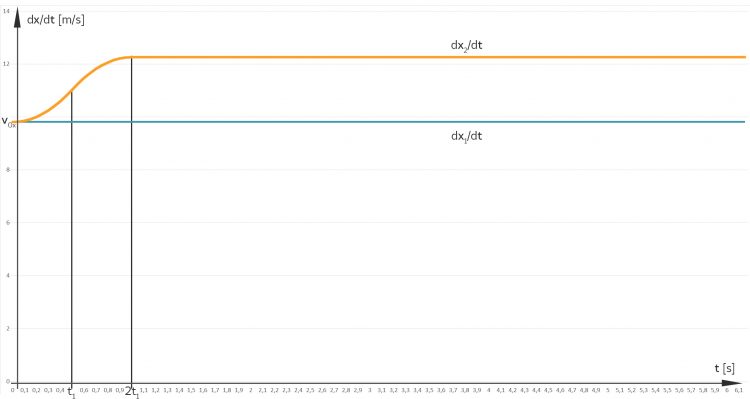
03_2019-kurve-handball_02_03
Geschwindigkeit der beiden Würfe mit den Werten wie oben.

***

Übungsaufgabe

Wie kann man den Wurf noch kraftvoller machen?

Lösung

ZB durch Vergrößerung von t1.