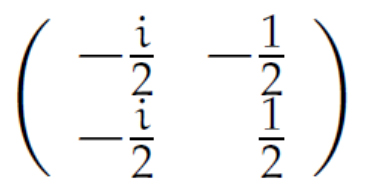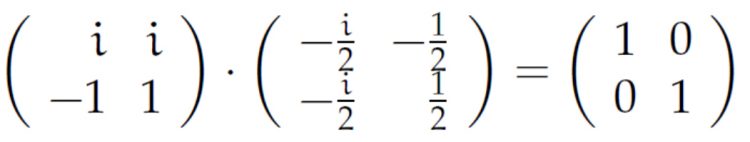Rike Dieses endlose Band finde ich nicht so motivierend. Ich fänd‘s schöner, eine lange Strecke geradeaus zu laufen, draußen natürlich.
Ben Ich auch.
Rike Weißt Du, wenn dieser Kreis hier in der komplexen Ebene wär, dann wüsste ich eine Transformation, mit der der Einheitskreis auf die Gerade abgebildet werden kann.
Ben Okay, die komplexe Ebene hat wohl viele tolle Eigenschaften?
Möbiustransformationen
Rike Ja, mit bestimmten Transformationen kannst Du

konform abbilden, und vor allem Kreise auf Kreise, Geraden auf Geraden, Geraden auf Kreise und umgekehrt.
Ben Hört sich gut an. Kannst Du denn auch so eine geeignete konstruieren?
Rike Klar! Zunächst sind Möbiustransformationen Verallgemeinerungen von linearen Transformationen
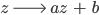
und Spezialfälle von Spiegelungen am Kreis
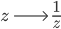
Allgemein heißt die Abbildung
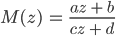
mit 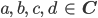 und
und
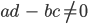
Möbiustransformation.
Ben Diese Bedingung
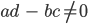
sieht wie eine Determinante aus.
Rike Richtig. Wenn diese Bedingung erfüllt ist, dann wird die komplexe Ebene auf sich abgebildet, sogar differenzierbar.
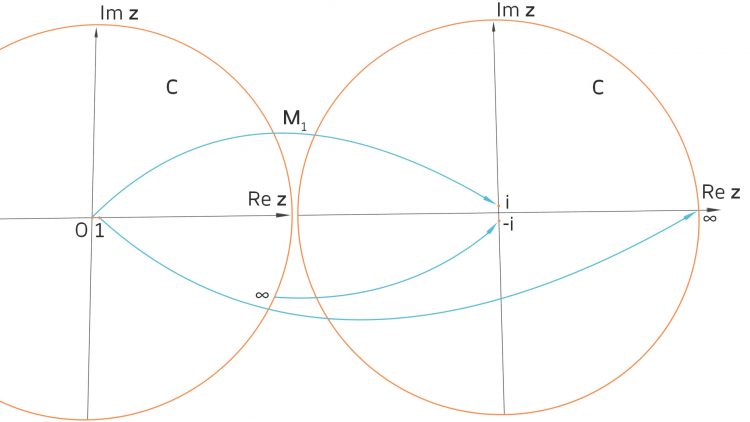
Eine konkrete Transformation
Lass uns mal
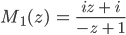
nehmen. Dann sind die Bilder M1(z) für
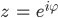
alle reell und z = 1 wird auf den unendlichen Punkt abgebildet.
Ben Was?
Rike Ja, z = 1 kommt bei der Abbildung M1 nach unendlich.
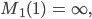
Im Komplexen gibt es nur ein Unendlich, nicht 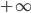 oder
oder 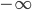 . Da ist Unendlich einfach der "Punkt" mit dem größten Radius.
. Da ist Unendlich einfach der "Punkt" mit dem größten Radius.
Ben Iss‘ ja cool. Warte mal, dann ist
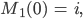
aber was ist 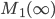 ?
?
Rike Dafür bilden wir einfach den Grenzwert für

Und das ist genau dann, wenn für
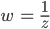

Ben Okay, dann versuche ich mal den Grenzwert zu bestimmen:
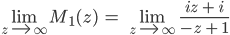
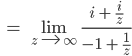
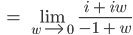
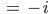
Rike Gut.
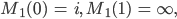 und
und 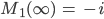 .
.Ben Aber wieso bildet Deine Transformation M1 den Kreis auf die Gerade ab?
Rike Das kann ich Dir zeigen. Wir nehmen für z nur Punkte auf dem Einheitskreis
und berechnen 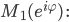
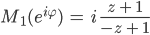
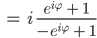
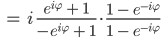
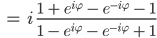
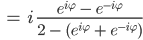
Das können wir prima mit den Eulerformeln vereinfachen:
Eulerformeln
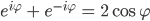
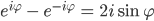
Ben Okay.
Rike Weiter gehts:
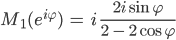
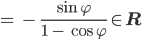
Ben Gut.
Rike Also die Bildpunkte des Kreises liegen auf der reellen Achse.
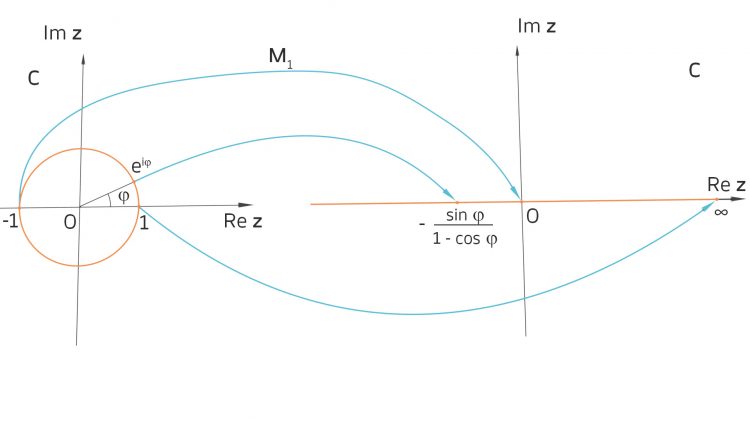
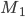 transformiert den Einheitskreis auf die reelle Achse.
transformiert den Einheitskreis auf die reelle Achse.Ben Gut, verstehe. Und wie geht das wieder zurück?
Inverse Transformation
Rike Du hattest schon die richtige Idee. Du nimmst die dazugehörige Matrix
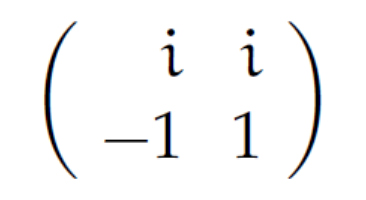 und berechnest dazu die Inverse. Das gibt
und berechnest dazu die Inverse. Das gibt
Ben Stimmt,
Rike Die inverse Transformation M2 zu M1 ist
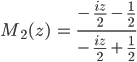
Jetzt nehmen wir reelle Argumente:
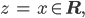
und berechnen den Betrag von M2(x):
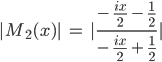

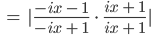
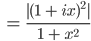
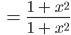
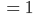
Ben Okay. Iss‘ ja cool. Aber vielleicht sind wir mit dem Kreis doch besser dran als mit der reellen Zahlengeraden? Nach dem Kreis könnten wir noch was unternehmen, nach der Gerade doch wohl nicht mehr?
Rike Hahaha
***
Übungsaufgaben
- Zeige, dass für
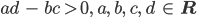 die Abbildung
die Abbildung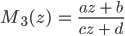
die reelle Achse in sich abbildet.
- Wo liegt M3(i) ?
Lösungen
- Für
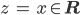 ist offensichtlich
ist offensichtlich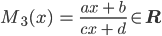
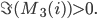 Der Bildpunkt liegt in der oberen Ebene.
Der Bildpunkt liegt in der oberen Ebene.