Max hat Stefan Kretzschmars Buch „Hölleluja!“ verschlungen. Lila fragt ihn, was er denn liest, Max erzählt von dem bekannten deutschen Handballspieler Stefan Kretzschmar, „Kretzsche“ genannt. Er ist sein Handballvorbild. Aber wie übersetzt man „Wenn es nicht kracht, ist es nicht Handball“ (Pos. 202) ins Englische? Einfacher ist schon „Austeilen, einstecken, sich fetzen und wieder vertragen“ (Pos. 4589). Jetzt bekommt er richtiges Heimweh, an seine noch zu werfenden 53 Tore ist gar nicht zu denken...
Lila kennt sich mit Handball nicht so gut aus. Sie fragt ihn, ob er Alfred Döblin kennt und sein Manas-Epos. Sie hat es in Englisch gelesen und war sehr angetan davon. Max kennt Alfred Döblin nicht. Doch nun muss er endlich nach Hause, seine Abschlussarbeit zu Ende bringen.
Als er auf seinen Flug wartet, findet er in der Wartehalle zufällig Berlin Alexanderplatz von Alfred Döblin. Und, was noch erstaunlicher ist, Franz Biberkopf, der seine Freundin Ida erschlagen hat, hat eine Formel für das Zuschlagen gefunden. Dort steht auf S. 99-100:
Biberkopfs Schreibweise
„Das erste Newtonsche (njutensche) Gesetz, welches lautet: Ein jeder Körper verharrt im Zustand der Ruhe, solange keine Kraftwirkung ihn veranlaßt, seinen Zustand zu ändern (bezieht sich auf Idas Rippen). Das zweite Bewegungsgesetz Njutens: Die Bewegungsänderung ist proportional der wirkenden Kraft und hat mit ihr die gleiche Richtung (die wirkende Kraft ist Franz, beziehungsweise sein Arm und seine Faust mit Inhalt). Die Größe der Kraft wird mit folgender Formel ausgedrückt:
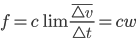
Die durch die Kraft bewirkte Beschleunigung, also den Grad der erzeugten Ruhestörung, spricht die Formel aus:
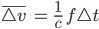
…“
Ja richtig, denkt Max, die newtonschen Gesetze. Heute schreibt man das so:

Doch warum hat Biberkopf den Grenzwert in der 2. Formel weggelassen? Wenn er in den beiden Gleichungen nach der Kraft f auflöst und diese Ausdrücke gleichsetzt, kriegt er
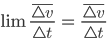
Der Querstrich steht vielleicht für einen Geschwindigkeitsvektor? Den lässt er jetzt mal weg und denkt sich, dass v erstmal für eine bestimmte Richtung steht – am besten die Wurfrichtung. Der Grenzwert der Differenzenquotienten entspricht die Ableitung nach der Zeit:
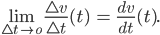
Differenzenquotient
Die Ableitung soll mit dem Differenzenquotienten übereinstimmen:
(1)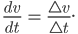
Irgendwie kommt er jetzt nicht weiter, er stöhnt. Da spricht ihn der Herr mit der Brille an:
Walter Entschuldigung, kann ich helfen? Mein Name ist Otto Walter.
Max Oh, ich versuche gerade ein mathematisches Problem zu lösen… Ich bin Max Ritter. Ich habe hier diese Gleichung und weiß nicht weiter.
Walter Oh, für den Differenzenquotienten müssen wir was Geschicktes einsetzen. Am besten, hm, nehmen wir die rückwärtige Differenz:
Diskretisierung
(2)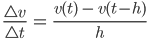
für ein h > 0. Dann kriegen wir aus der Gleichung (1) mit dem Ansatz (2):
Retardierte Dgl
(3)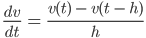
Das nennt sich retardierte Gleichung. Die Änderung von v zur Zeit t wird durch v(t) und v(t-h) gegeben. Die Änderung der Geschwindigkeit wird durch die Geschwindigkeit v(t) und die Geschwindigkeit zu einem früheren Augenblick v(t - h) bestimmt.
Max Hmm, ist ja eigenartig, so eine Verzögerung. Okay. Können Sie die lösen?
Walter Ich denke schon. Wie sind denn Ihre Anfangswerte? Also für diese Art von Gleichungen brauchen Sie v(t) für
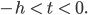
Das nennen wir mal v0(t).
Max Wenn die Geschwindigkeit konstant ist, dann entsteht keine Kraftwirkung, 1. newtonsches Gesetz. Hm, dann nehmen wir vielleicht statt einer Konstanten eine Funktion mit einem linearen Anstieg?
Anfangswertproblem
Walter Gut, lassen Sie uns
(4)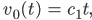
für
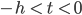
und mit
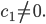
nehmen. Das setzen wir statt v(t-h) ein und lösen die Differenzialgleichung ein kleines Stück – nämlich für 0 < t < h. Die Funktion v heißt dann v1, das ist v im 1. Stück. Das heißt v0 und ist die Vergangenheit von v1, v1 wird dann die Vergangenheit von v2 usw. Man löst das stückweise.
Stückweises Lösen
Max Verstehe. Sind Sie etwa zufällig Spezialist für retardierte Gleichungen?
Walter Ja, das kann man so sagen, das war mal mein Arbeitsgebiet. Ich finde in Allem retadierte Dgln. Naja, fast. Weiter!
Max Wir kriegen dann
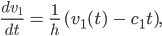
für
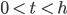
Walter
Das ist eine lineare inhomogene Dgl. Man löst die homogene, das sieht man quasi:
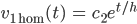
und variiert nun die Konstante, dh.
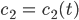
Das setzt man in die Dgl ein und kriegt
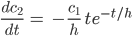
Max Okay, das muss ich nur noch integrieren. Gut, das ergibt mit partieller Integration
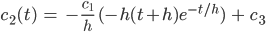
und als Lösung der Dgl. kriege ich
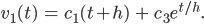
Walter Jetzt müssen wir noch die Konstante c3 bestimmen. Wir haben die Anfangsbedingungen noch nicht benutzt. Wenn wir bei v0 die Zeit nach t = 0 gehen lassen, kriegen wir
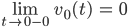
Max Verstehe.
Walter Das benutzen wir, v1 soll ja schließlich stetig bei t = 0 beginnen.
Max Gut, dann kriegen wir
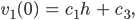
das soll Null sein. Das ergibt
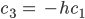
und
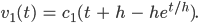
Schön!
Lösung im 2. Zeitabschnitt
Walter Jetzt können wir dieses v1(t) als Vergangenheit für v2(t) mit
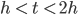
nehmen. Die Dgl ist dann in diesem Zeitbereich
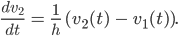
Wir setzen das ein, lösen die homogene Dgl, das ergibt wieder
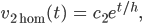
Wir variieren die Konstante c2 und kriegen nach ein bisschen Rechnung
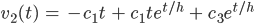
Wir suchen den Grenzwert für t = h für v1 und nehmen das als Anfangswert für v2. Das ergibt, Moment,…, ja jetzt hab‘ ich’s:
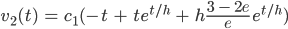
für
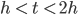
und immer so weiter.
Max Danke, Herr Walter. Jetzt würde ich das gerne mal zeichnen für meinen Fall. Die Geschwindigkeit setze ich vorm Aufprall
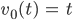
Können wir

nehmen?
Walter Klar, h muss nicht klein sein.
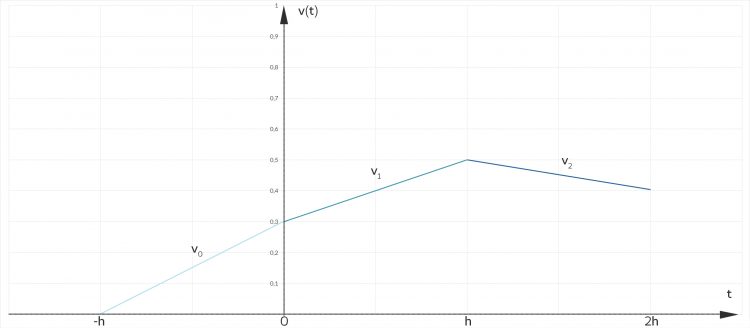
Max Moment, dann erhalte ich solche Kurven:
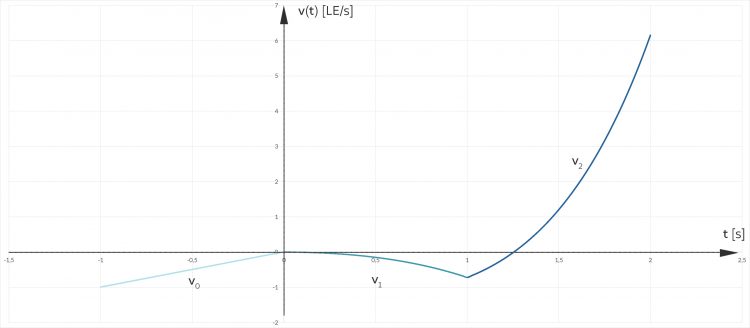
Hm, ziemliche Dynamik, wie geht's weiter? Für v3 muss ich
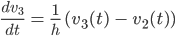
lösen. Die "Vergangenheit" v2 "holt" die Funktion v3 nach "unten". Ist ja ziemlich kompliziert. Ob Biberkopf das wirklich gemeint hat? Oder Kretzsche?
Walter Hahaha, guten Flug nach Hause!
Max Ebenso.
***
Übungsaufgaben
- Prüfe den Ansatz für
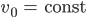
- Wie ändert sich die biberkopfsche Lösung, wenn sich die Konstante c1 ändert?
- Bestimme v3.
Lösungen
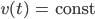
- Die Konstante c1 geht als Faktor in die Lösung ein.
