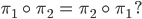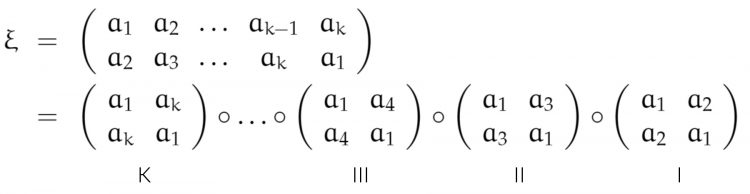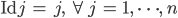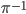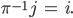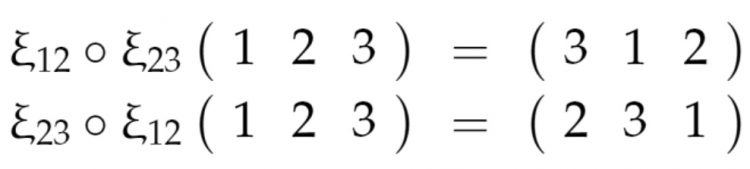Sitzplatzpermutationen

Ben und Rike sitzen im Flieger und fliegen nach Hause. Wird ja auch Zeit, das Weihnachtsfest … Plötzlich knallt es. Es gibt einen ohrenbetäubenden Lärm, Ben wird von seinem Sitz hochgeschleudert und landet auf dem Nachbarsitz. Die anderen Fluggäste werden auch jeweils weiter zum nächsten Sitz expediert. Nur Rike nicht. Sie lacht.

Ben Was lachst Du?

Rike Die Sitzplatzpermutationsgruppe!

Ben Was?

Rike Ihr seid alle einen Platz weiter gerückt. Dieses Weiterrücken ist eine Aktion, dazu gibt es eine Gegenaktion, die das Weiterrücken vom Platz

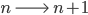
rückgängig macht.

Ben Klar, von n+1 auf n.

Rike Richtig! Und die „Nullaktion“, wo keiner weiterrückt, ist die Identität:

n wird auf n abgebildet.

Ben Was ist die Permutationsgruppe? Wir hatten wenig lineare Algebra im Studium.

Rike Zunächst gibt es den Gruppenbegriff:

Gruppe

Eine Menge G mit einer Verknüpfung von 2 Elementen g₁ und g₂ von G

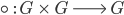
muß definiert sein, also

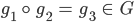
ist immer ausführbar.

1-Element

Es gibt ein 1-Element 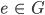sodass

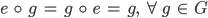
Inverses

Und als Letztes soll zu jedem 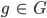stets ein „Inverses“ 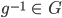existieren, sodass

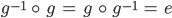
Ben Na, gut. Gibt’s triviale Beispiele?

Rike Die ganzen Zahlen mit der Addition als Verknüpfung oder die Restklassen mit der Restklassenaddition.

Ben Gut. Und die Permutationsgruppe?

Rike Die Permutationsgruppe P_n ist die Menge der bijektiven Abbildungen der Menge

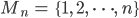
auf sich.

Ben Okay, dann gibt es n! Permutationen.

Rike Stimmt! Die Permutationsgruppe ist eine endliche Gruppe. Sie hat wirklich schöne Eigenschaften. Schau mal, wenn 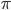eine Permutation ist, dann bildet 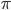M_n auf M_n ab,

Permutation in Komponentenschreibweise

und komponentenweise kann man das so schreiben:

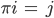
Oder man kann es gleich auf die ganze Menge M_n anwenden und schreibt das mit einer Matrix:

Permutation in Matrixschreibweise

Vereinfachte Schreibweise

Es ist üblich, die Spalten, die invariant bleiben, also für die

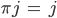
ist, in der Matrix wegzulassen.

Verknüpfung in P_n

Die Verknüpfung in P_n ist die Nacheinanderausführung der Abbildungen. Das geht so: Wenn

und

sind, dann soll die Verknüpfung von 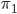und

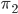
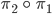
die Permutation 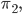angewendet auf die Permutatio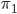n sein:

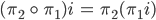
komponentenweise oder in Matrixschreibweise:

Ben Hm, das lässt sich gut programmieren.

Rike Ja, lass uns mal aufschreiben, was jetzt passiert ist, sagen wir mal, wir haben 100 Sitzplätze,

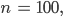
und jeder Inhaber eines Platzes ist eins weitergerückt, außer mir, ich habe den Platz 1, aber nur heute im Flugzeug, Ben, dann schreibt sich das als

Ben Okay. Ich bin vom Platz Nr. 2, aber nur heute, Rike, zu Platz Nr. 3 gekommen.

k-Zykel

Rike Für solche „Weiterrück-Permutationen“ gibt es einen Begriff: Wenn k von n Elementen immer eins weitergerückt werden:

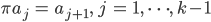
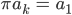
oder in Matrixschreibweise:

so heißt das k-Zykel.

Ben Okay, wir haben gerade einen 99-Zykel erlebt.

Transposition

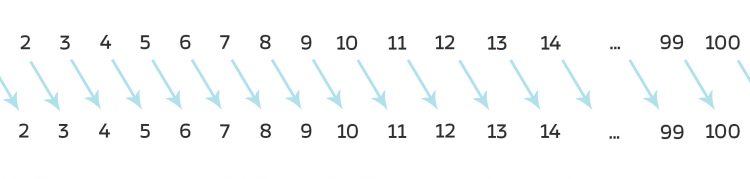
Rike Richtig. Den einfachste Fall eines k-Zykels haben wir für k = 2, also wenn sich zwei Elemente vertauschen:

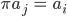
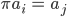
das heißt Transposition. In Matrixschreibweise geht das so:

Ben Sind das nicht ganz unterschiedliche Dinge? Beim k-Zykel rücken alle „Beteiligten“ eins weiter, ihre relative Ordnung bleibt bestehen, bei der Transposition werden zwei Plätze getauscht, ihre Ordnung wird umgekehrt. Hier bei dem Bild war erst das 6. Element vor dem 7. Nach der Transposition ist das 7. Element vor dem 6.?

Rike Ja, das sieht so aus. Aber höre, Ben, es gibt einen Zusammenhang von beiden, Du kannst nämlich jeden k-Zykel als Produkt – also als Nacheinanderausführung von Transpositionen schreiben!

Ben Das glaube ich nicht!

Rike Doch! Dieses Produkt kann ich Dir sogar konstruktiv nennen:

Ben Warte mal, zuerst tauscht Du die ersten beiden Teilnehmer des Zykels. Das zweite Element geht an die Stelle des ersten und das erste an die Stelle des zweiten. Danach tauschst Du die 1. und 3. Stelle, dann steht das 3. Element wieder hinter dem 2. usw. Ist ja krass!

Flugzeugbeispiel

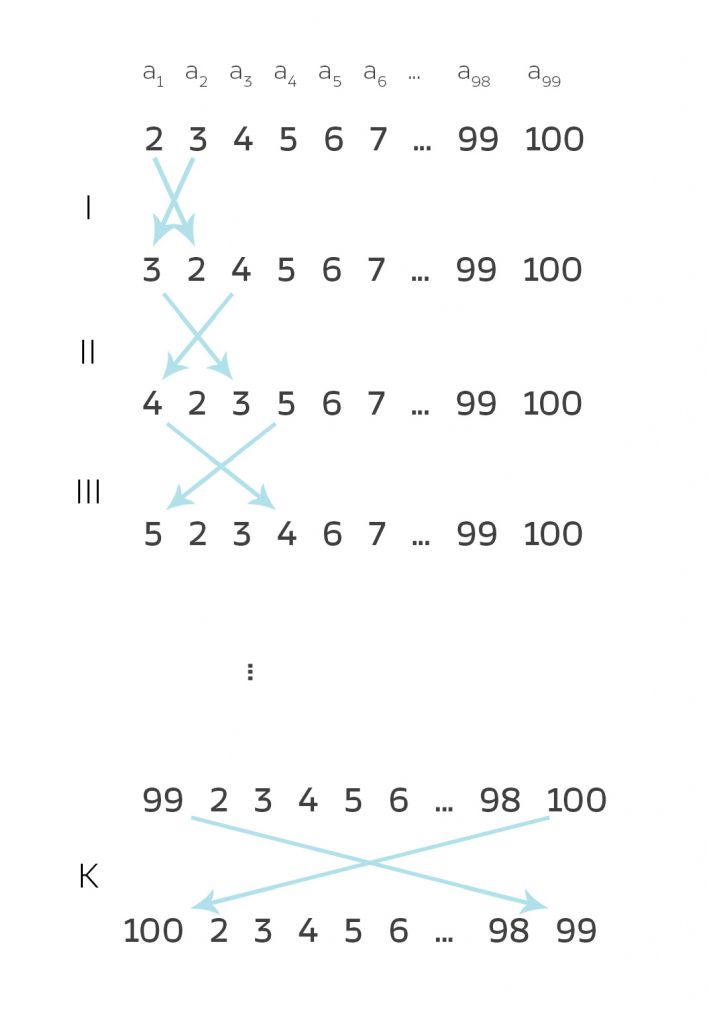
Kann man eigentlich jede Permutation als Produkt von Transpositionen schreiben?

Rike Ja!

Ben Das ist ja cool. Dann kann man das eigentlich gut für einen Sortieralgorithmus benutzen, man zerlegt jede Sortierung  in seine elementaren Bestandteile, die Transpositionen, das ist überschaubar und gut programmierbar!

Übungsaufgaben

1. Prüfe die Gruppeneigenschaften für die Permutationsgruppe.
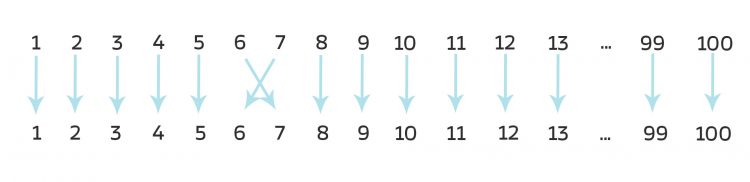
2. Ist P_n kommutativ, das heißt, da ist

Lösungen

1. P_n ist eine Gruppe mit dem Einselement Id:

   und dem zu einer Permutation mit

   inverser Permutation mit

2. Nein, P_n ist nicht kommutativ, denn für die Transpositionen

   
   und
   ist