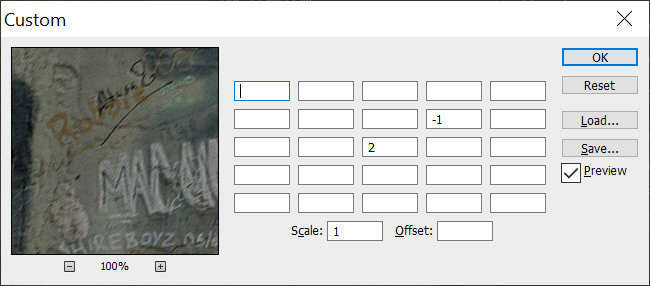
Jule und Rike machen einen Spaziergang durch Berlin. Es regnet heftig. Jule interessiert sich für Graffitis. In Berlin gibt es besonders viele, da kann ihre Unistadt Duisburg nicht mithalten. An der Berliner Mauer in Friedrichshain findet sie eins, das ihr besonders gut gefällt. Jule und Rike bitten einen Passanten, ein Mauerfoto mit ihnen zu machen. Doch der Regen ist zu stark. Jule macht Fotos vom Graffiti an der Mauer.
Jule Rike, das Mauerbild ist richtig gut. Schade, dass es gerade jetzt regnet. Sieh mal hier:

Alles ist leicht verwischt. Kann man das retten?
Diskrete Faltung für Bilder
Rike Mal sehen. Wenn man genau hinsieht, kann man den Winkel vom Regen herausfinden, sagen wir mal 45°. Durch die Brechung des Lichtes an den einzelnen Tropfen und noch dazu der Bewegung der Tropfen überlagern sich die Informationen jedes Pixels. Zu jedem Pixel wird sein Pendant von rechts oben addiert – mit einem Gewicht, das die Stärke der Verwischung ausmacht. Und wenn man das allgemein aufschreibt, dann ist das
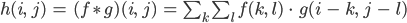
Und das ist gerade die Diskretisierung der Faltung für die Funktionen  und
und 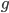 , die nur auf Punkten erklärt sind.
, die nur auf Punkten erklärt sind.
Jule Okay, solche Diskretisierungen hatten wir schon. Hier ist das 2-dimensional?
Rike Ja, 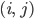 gibt gerade die Position eines Pixels an.
gibt gerade die Position eines Pixels an.
Jule Und was sind 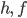 und
und 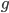 ?
?
Rike 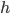 und
und 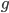 beschreiben jeweils die Information für jedes Pixel, zum Beispiel die Farbinformation in einem Kanal oder die Helligkeit bei einem Schwarzweißbild:
beschreiben jeweils die Information für jedes Pixel, zum Beispiel die Farbinformation in einem Kanal oder die Helligkeit bei einem Schwarzweißbild: 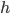 nach dem Falten und
nach dem Falten und 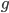 steht für das Ausgangsbild.
steht für das Ausgangsbild.  ist der Faltungskern.
ist der Faltungskern.
Jule Na gut. Und weiter? Jetzt haben wir das praktische Ergebnis einer natürlichen Faltung. Und wie geht das jetzt zurück? Kannst Du das?
Faltungsmatrix
Rike Sei doch nicht so ungeduldig. Wir überlegen erst mal, wie der Kern Deiner praktischen natürlichen Faltung aussieht. Diesen Kern kannst Du als Matrix schreiben. Tatsächlich ist das schon in Photoshop umgesetzt. Es ist leider ohne künstliche Intelligenz, ganz auf Pixelbasis. Ich zeige Dir das mal. Die Matrix mit der 1 in der Mitte und sonst Nullen verändert gar nichts.
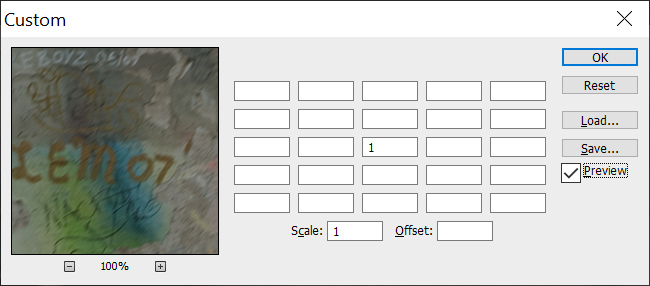
Sie wirkt auf jeden Punkt an der Stelle 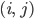 wie die Identität.
wie die Identität.
Jule Ich blicke noch nicht durch. Wie rechnest Du die Faltung nun aus?
Rike Mit der Faltungsformel. Sie wird punktweise auf jeden Pixel angewendet.
Jule Okay. Dann wird die Information jedes Pixels mit 1 multipliziert und ein paar Nullen addiert? Haha!
Verwischung
Rike Richtig. Jetzt kommt die Wirkung unseres Regens! Ich schätze, dass an jedem Punkt der Wert seines rechten oberen Nachbarn addiert wird, aber nicht mit demselben Gewicht, sondern schwächer. Nehmen wir mal an: 2x der Originalpunkt plus 1x der Nachbar, so:
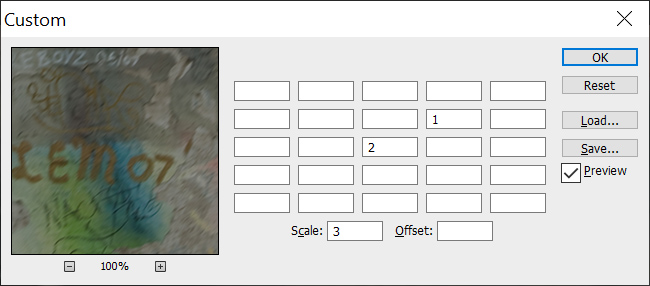
Jule Na gut, verstehe. Was ist das mit der 3?
Rike Das ist eine Skalierung, durch den Skalierungsfaktor teilen wir das Ergebnis. Wenn wir nicht skalieren, kommt an die Stelle des originalen Farbwertes dann der zweifache Wert plus der vom Nachbarn, dann wird es ziemlich hell.
Jule Verstehe. Das ist die Summe der einzelnen Gewichte?
Rike Stimmt!
Umkehrung der Verwischung
Jule Klar. Und jetzt die Umkehrung! Wir ziehen vom Originalwert den Wert vom rechten oberen Nachbarn ab? Mit einem Gewicht? 2:1?
Rike Lass uns das mal probieren! Ooh, nein, das schärft viel zu stark! Lass uns was anderes nehmen, ich muss das ausprobieren, hier, das klappt gut.
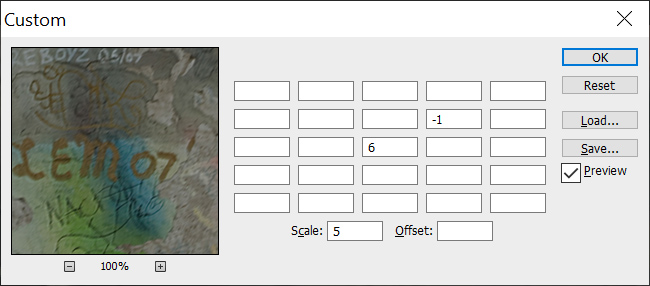
Diese Faltung wende ich nun mehrfach an. Du hattest eine Weichzeichnung in eine Richtung von ca. 10 Pixeln, und nach 10 x Faltung mit dieser Matrix bekomme ich:

Jule Danke Rike, ich find‘s super, jetzt kann ich fast alle Inschriften lesen, für mich ist das erstmal okay!
***
Übungsaufgaben
- Teste selbst die zehnfache Anwendung der Faltung auf das obige „Regenbild“!
- Was erhält man bei zehnfacher Anwendung mit dem Verhältnis 2:1, wie von Jule vorgeschlagen?
- Warum klappt dieses Verhältnis nicht?
Lösungen
2. Man erhält nach 10-facher Anwendung der Faltung auf das oberste "Regenbild" mit
das Resultat:
3. Für einen Beispielpunkt 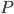 im Bild mit
im Bild mit
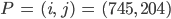
und den RGB-Werten
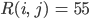
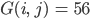
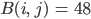
und seinem rechten oberen Nachbarn
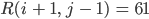
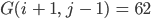
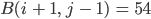
erhält man nach einmaliger Anwendung
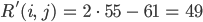
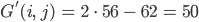
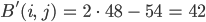
Die neuen Farbwerte unterscheiden sich wesentlich von den alten, sie werden kleiner statt größer.
Copyright für das originale Bild
Eddie Gerald / Alamy Stock Foto, 21.06.2008.