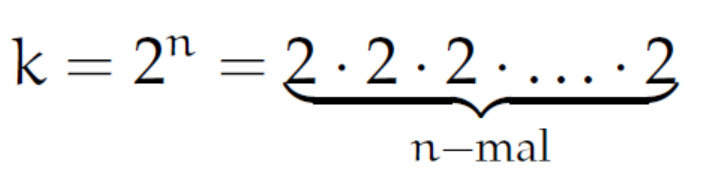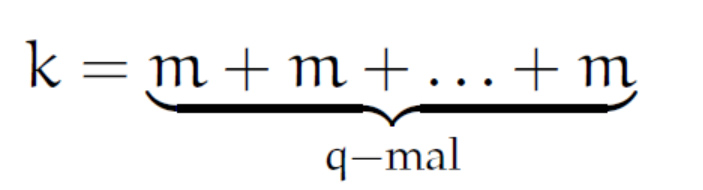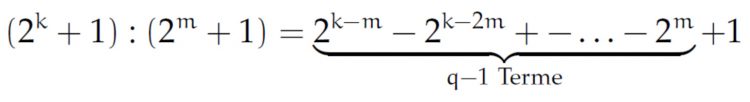Lila will nach ihrem Deutschkurs einen Kaffee in der Mensa trinken. Dort lernt sie Jenny kennen. Jenny holt sich auch Kaffee, um für ihre nächste Matheprüfung zu lernen. Sie erzählt von ihrer bevorstehenden Prüfung, Lila berichtet von ihrer Berechnung von Mersenne-Primzahlen.
Jenny Sag mal, wenn Du die Mersenne-Primzahlen kennst, dann kennst Du doch auch die Fermat-Zahlen?
Lila No, ich bin zufällig zum GIMPS-Projekt gekommen. Ich wollte einfach mal eine nützliche Zahl mitausrechnen. Ich habe keinen zahlentheoretischen Background. Es hat mir Spaß gemacht, und jetzt will ich in Berlin was in der Richtung studieren.
Jenny Lila, da bist Du hier richtig! Berlin bietet viele Möglichkeiten, wir haben mehrere Unis mit verschiedenen Ausrichtungen. In meinem Studium war bis jetzt nicht viel Zahlentheorie. Im ersten Semester hatten wir lineare Algebra. Ich habe mich nicht so gut in das algebraische Denken hineingefunden – wie die meisten von uns. Da habe mir ein Algebra-Buch gekauft. Es hat mir gefallen – und weißt Du, was darin die erste Übungsaufgabe war?
Lila Na?
Mersenne- und Fermat-Zahlen
Jenny Die Mersenne- und Fermat-Zahlen zu untersuchen. Ich hatte große Schwierigkeiten damit, aber dann habe ich's geschafft. Wenn ich diese Aufgabe nicht gelöst hätte, dann hätte ich vielleicht aufgegeben!
Lila Und wie lautete die Aufgabe genau?
Jenny Die Mersenne-Zahlen haben die Gestalt:
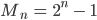
Einige von denen sind Primzahlen, das weißt Du ja schon. Die Fermat-Zahlen sehen so aus:
von denen sind auch einige Primzahlen. Die Übungsaufgabe 1.1.1 in meinem Lieblingsbuch geht so: Beweisen Sie die folgende Eigenschaft:
Satz 1
Wenn eine Zahl
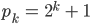
prim ist,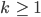 
und natürlich, dann muss 
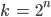sein.
Lila Okay. Zuerst lass mich ich ein paar Beispiele testen.
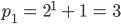
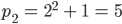
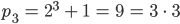
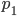und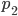 
sind Fermat-Zahlen und Primzahlen, okay. 
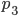ist keine Primzahl, stimmt's?
Jenny Ja!
Lila 3 ist keine Zweierpotenz, also ist 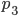keine Fermat-Zahl. Gut.
Jenny Ja, so geht es immer weiter. Ich habe versucht herauszufinden, durch welche Zahlen die pk‘s zu teilen sind, wenn 
keine Zweierpotenz ist. Und ich habe zuerst die Primfaktorzerlegung dafür entdeckt und dann einen Zusammenhang gesucht, sieh mal:
Jennys Test
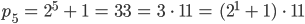
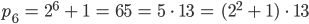
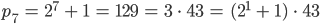
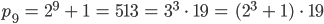
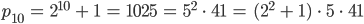
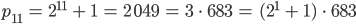
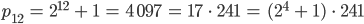
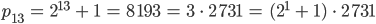
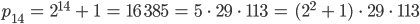
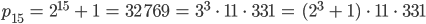
Lila, findest Du ein Bildungsgesetz zwischen dem Index und dem Exponenten für die 2 auf der rechten Seite?
Beweis von Satz 1
Lila Warte‚ mal, der Exponent ist Teiler von ?
Jenny Richtig! Du musst zeigen, dass diese Zahlen pk, wo keine Zweierpotenz ist, eine nichttriviale Primfaktorzerlegung haben. Ich glaube, wir haben sie schon fast entdeckt. Zuerst zerlegst Du ebenfalls in Primfaktoren. Wenn eine reine Zweierpotenz wäre, hätten wir
Ist nun keine Zweierpotenz, dann muss seine Primfaktorzerlegung eine ungerade Primzahl enthalten, die nennen wir mal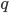 
, und den Rest fassen wir zu 
zusammen:
Ansatz und Beweisidee
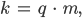
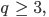prim, 
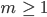. Ja?
Lila Okay.
Jenny Das bedeutet auch, dass man so zerlegen kann:
Lila Ist doch klar, wozu brauchst Du das?
Jenny Schön, dasss das für Dich klar ist, ich bin lange nicht 'drauf gekommen, das Produkt als Summe zu schreiben. Das benutzen wir gleich. Jetzt kannst Du
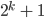
durch
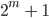
teilen.
Lila Okay. Das durchschaue ich jetzt nicht.
Jenny Da machst Du so eine Art "schriftliche Division" und kriegst:
Weil 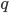ungerade ist, ist 
gerade, nur so geht diese Division mit den wechselnden Vorzeichen auf und endet mit "+1". Das heißt, die Zahlen pk mit
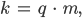
sind nicht prim, sie haben eine nichttriviale Produktdarstellung:
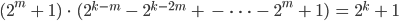
Lila Wow! Hast Du das allein herausgefunden?
Algebra als Herausforderung
Jenny Ja, aber ich habe eine Woche dran gesessen! War schon die Härte für mich.
Lila Okay! I know. Es sieht so einfach aus, und Du siehst es doch nicht. Es ist irgendwie anders als Programmieren und Schulmathematik.
Jenny Ja. Dieses algebraische Denken, das ist nicht so straightforward, da musst Du in Strukturen denken und so eine Art Gefühl entwickeln.
Lila Was, ein Algebra-Gefühl? Haha!
Jenny Ja, sowas. Ich habe eine ganze Weile gebraucht, mir war, als wäre ich draußen und kein Weg geht rein, als wäre ich nicht gut vorbereitet darauf, als müsste ich ... ach ich weiß auch nicht!
Lila Hmm, ich weiß nicht, ob ich das schaffe.
Jenny Why not? Lass uns weitermachen, das ist der beste Weg.
Lila Na gut, dann weißt Du jetzt, dass für ’s, die keine Zweierpotenzen sind, die Zahlen pk eine Produktzerlegung haben und nicht prim sind.
Jenny Ja, jetzt bist du fertig! Nur die Zahlen pk mit der Struktur der Fermat-Zahlen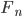 
haben eine Chance, Primzahl zu sein. Das war ein indirekter Beweis!
Lila Oooh! Sag mal, kann man denn da noch welche bestimmen? Ich programmiere ganz gern.
Jenny Hahaha, ja, wollen wir uns noch mal treffen? Ich muss jetzt los!
Lila Klar, hier ist meine Handynummer! Tschüß!
***
Übungsaufgabe
- Mache die Probe für die Divison
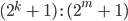
- Finde Zahlen, die Mersenne-, Fermat- und Primzahlen sind!
Lösung
- Durch Ausmultiplizieren
- Nur die 3, denn es sind bisher nur die Fermat-Primzahlen
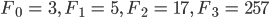und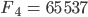 
bekannt.