Rikes Schwester Jule kommt nach Berlin, um Rike und Ben zu besuchen. Außerdem hat sie ein kleines IT-Problem mitgebracht. Sie hat in einer Zeitung ein Foto von der Lemgoer Skatebahn gefunden – mit einem Graffiti ihres Freundes Nico, dem besten Sprayer überhaupt, was nun übermalt wurde. Zu gern würde sie das Bild rekonstruieren.
Jule Kannst Du mir weiterhelfen?
Algorithmen zur Bildrekonstruktion
Rike Ich versuch’s. Wir haben in letzter Zeit die Arbeiten von Mitra und Kollegen zum Deep Learning in der Bildverarbeitung verfolgt. So gibt es Algorithmen des tiefen Lernens, die nicht pixelweise funktionieren, sondern inhaltlich. Mit solchen Methoden versuchen sie, in diesem Bild Kanten zu finden, Tiefeninformation sowie Flächen zu entdecken. Dabei wird das Rauschen unterdrückt bzw. vernachlässigt.
Wenn diese Informationen gefunden wurden, wird das kleingerechnete und auf das Wesentliche reduzierte Ausgangsbild mit den neuen, hochgerechneten Bildern mit den Kanten, erkannten Objekten, Tiefeninformation und Normalenrichtungen gefaltet. Dabei können sogar fehlende Bildteile rekonstruiert werden und es entsteht ein neues „fehlerfreies“, hochaufgelöstes Bild.
Faltung
Jule Was ist denn falten?
Rike Das ist so eine Art von Multiplikation von 2 Funktionen. Nehmen wir mal die Funktionen 
und 
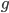. Beide sollen nur auf einer beschränkten Menge ungleich 0 sein, und natürlich integrierbar. Dann kannst Du die neue Funktion
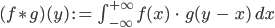
berechnen. Das ist die Faltung von und .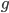
Jule Hmm. Überschaue ich nicht.
Rike Wir machen das mal eindimensional. Nehmen wir mal an, Du hast eine geometrische Information im Ausgangsbild: Das ist mal die Funktion , nehmen wir mal ein Rechteck, und Du hast eine Struktur 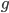entdeckt, nehmen wir mal ein weiteres Rechteck. Dann musst Du die Funktion 
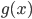spiegeln:
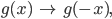
um 
verschieben:
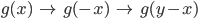
Diese Funktion multiplizierst Du mit für ein festes und integrierst dieses Produkt über 
. Wenn sich und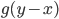 
nicht überlagern, dann ist das Ergebnis der Faltung 0. Wenn sie sich beim Verschieben von nach rechts zum ersten Mal treffen, dann wird die neue Funktion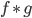 
anwachsen.
Jule Okay. Gut. Da entsteht so eine Art Rampe!
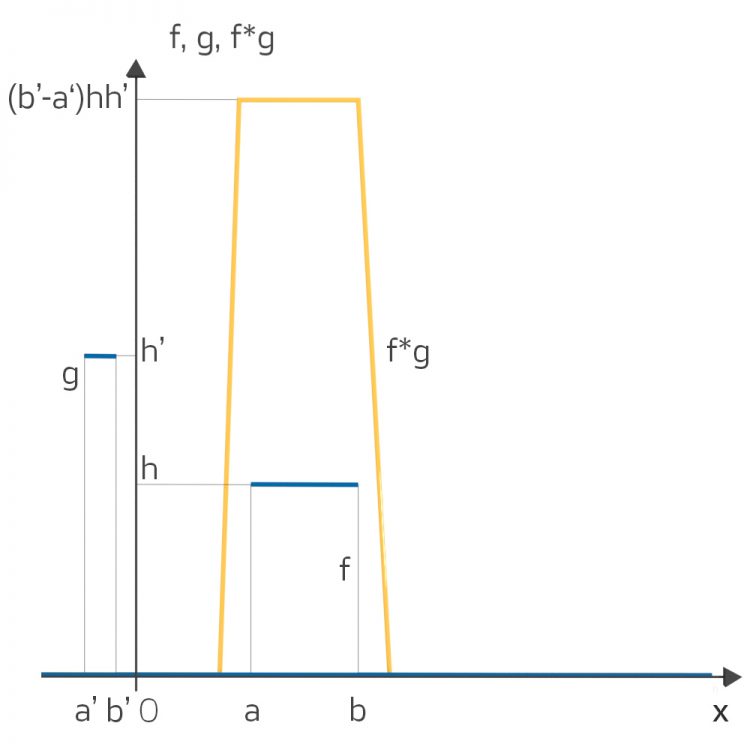
und 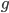und ihre Faltung 
Rike Stimmt!
Rekonstruktion in Jules Beispiel
Jule Und in der Rampe sind alle Informationen von und 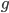enthalten. Hey, das ist gut. So kannst Du wirklich ein Bild vergrößern. Warte mal, ich versuche das mal zu programmieren. Zuerst gehe ich alle Pixel durch und suche die Tiefeninformation, okay, da muss ich die Unschärfe oder Weichzeichnung lokal vergleichen, hier:
Dann die Normalenrichtungen: Da brauche ich einen anderen Algorithmus, hier muss ich die Helligkeiten und Farbigkeiten lokal vergleichen, so:
mit Semantic Labeling, schreiben Eigen und Fergus, findet man die Geometrien im Bild. Das ist so eine Art pixelweise Informations- und Entropieberechnung.
Jule Echt stark! Und jetzt muss ich das mit dem Ausgangsbild geschickt falten, na gut, habt Ihr da was?
Rike Ja, ich hab‘ das mal probiert, warte, die fehlenden Stellen kann ich gut ergänzen, das sind ja nur Bäume, das geht mit Deep Learning, hier:
Jule Danke! Das gefällt mir, echt krass! Das rekonstruierte Bild ist viel cleaner und viel größer.
Rike Ja, das geht bis zur 4-fachen Größe!
Jule Diese Technologie hat enormes Potenzial! Echte Digitalisierung von Bildern! Rekonstrution eben auch. Mann! Ich schaue mir dann auch mal die Faltung an!
***
Übungsaufgabe
Was kann man aus der Faltung im Falle zweier Rechtecke rekonstruieren?
Lösung
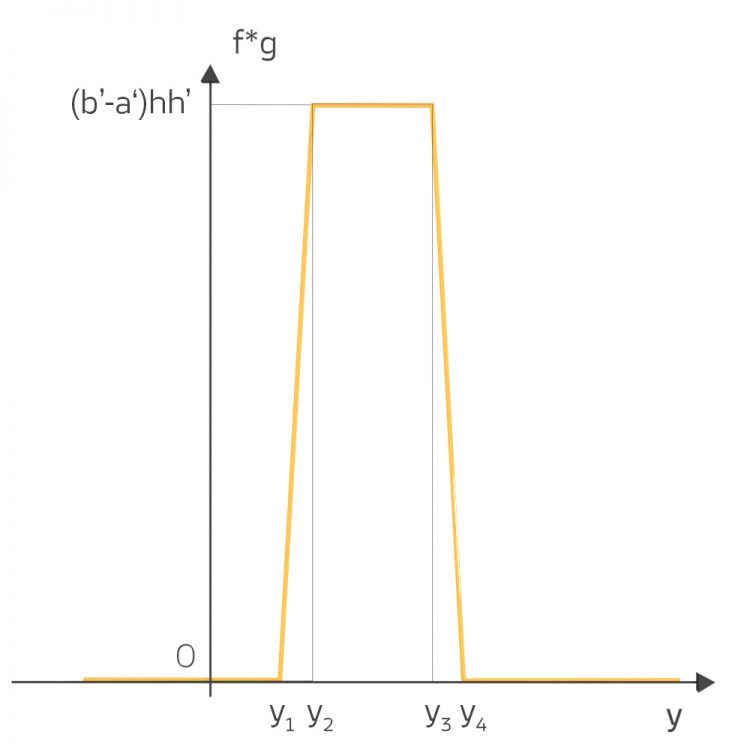
Die Funktion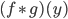 
hat die folgende Gestalt:
mit
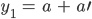
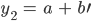
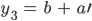
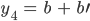
O.B.d.A. sei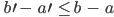 
.
Betrachtet man nun die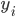 
in den 4 Gleichungen als gegebene rechte Seite und 
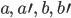als Unbekannte, so erhält man die Determinante 0 für die Koeffizentenmarix. Es sind nicht alle 4 Unbekannten eindeutig bestimmbar.
Ebenso kann man aus der Höhe der Ergebnisfunktion nicht die einzelnen Höhen bestimmen.
Sind allerdings 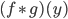mit der Höhe 
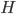und den Punkten 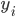sowie eine der Funktionen oder 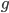gegeben, z.B. 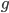mit der Höhe 
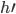und dem Träger 
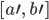, so ist daraus bestimmbar. ist eine Rechteckfunktion auf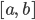 
mit der Höhe
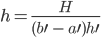
und
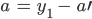
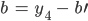
Das könnte man inverse Faltung nennen.
Dank
Die fotorealistischen Bilder sind im Sommersemester 2019 mit Fotos von Studierenden des 2. Semesters Medienproduktion entstanden.