Max und Rike haben eine Auszeit genommen und machen einen Ski-Urlaub in den Bergen. Max hat ein recht aufregendes Semester hinter sich und Rike arbeitet an einem Spiel (im hyperbolischen Raum). Rike ist mit ihren Gedanken immer noch bei ihrem Game. Dort gibt es eine virtuelle Kamera und kein Kamerahersteller dieser Welt kann ihr die technischen Daten für ihre virtuelle Kamera liefern. Also will sie selbst Erfahrungen sammeln (im euklidischen Raum).
Max Rike, wie schön es hier ist, Sonnenschein, klare Sicht bis zum Horizont!
Rike Ja, es ist wunderbar. Jetzt will ich ausprobieren, ob sich die Objekte am Horizont wirklich fotografieren lassen, ob sie sich auflösen. Was meinst Du, wie weit ist diese Hütte da am Lift da hinten von uns entfernt?
Max Wart mal, das kann ich mit Google-Maps herausfinden … es sind 5500 m.
Rike Okay, also da ist dann mein Fokus. Zur Berechnung des Schärfentiefebereiches gibt es Formeln und Anwendungen, die immer Angaben über den sogenannten Unschärfekreis, den Circle of Confusion, benutzen. Und die will ich jetzt überprüfen.
Max Okay, wie geht das?
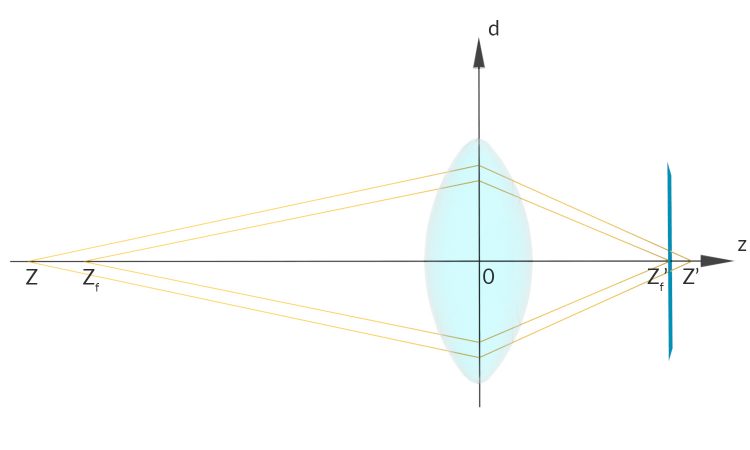
Rike Zuerst erinnern wir uns an die Linsengleichung. Die gilt zwar nur für dünne Linsen, doch wir schauen mal, wie das klappt.
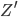ist der Bildpunkt von 
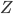. Beachte 
Die Linsengleichung
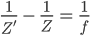
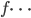
Max Okay.
Rike Das kann man nach 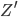umstellen und erhält
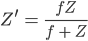
Max Okay.
Rike Das gilt natürlich auch für den Fokuspunkt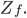 
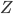Bei liegt der Punkt, den wir fotografieren, bei 
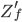ist die Bildebene, auf die wir abbilden. 
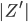ist dann die Entfernung des Bildpunktes vom optischen Mittelpunkt der Linse aus gemessen.
Fokuspunkte
Hier ergibt die Linsengleichung
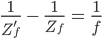
Max Okay.
Rike Das können wir wieder umstellen nach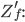 
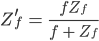
Max Okay, und weiter?
Circle of Confusion
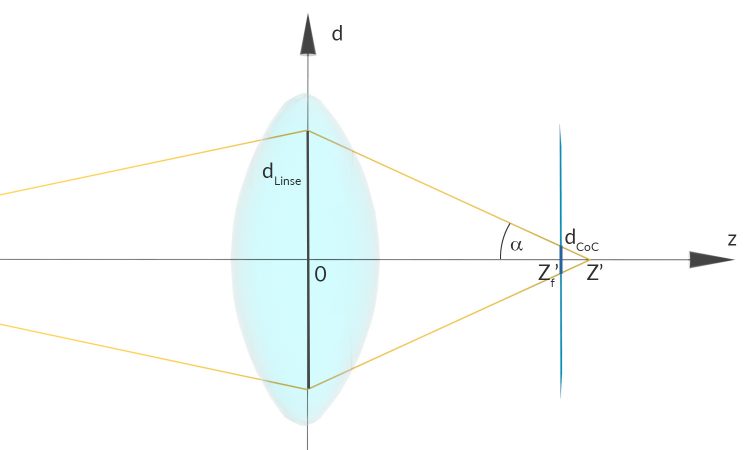
Rike Jetzt überlegen wir mal, was dieser Circle of Confusion ist.
Max Na, das ist der Durchmesser des kleinsten “scharfen” Kreises im Bild.
Rike Okay, weißt Du, das bedeutet, dass man bei 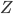einen Punkt hat, 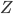ist nicht im Fokus!, und der wird in der Bildebene zum Kreis.
Max Stimmt, dieses Circle of Confusion muss ja vom Abstand 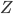abhängen, hatte ich bisher nicht beachtet.
Rike Wenn wir dann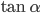 
berechnen, erhalten wir:
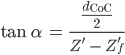
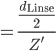
Max Okay, is' ja cool.
Rike Das stellen wir nach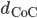 
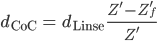
Für 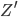benutzen wir die Formel, die wir aus der Linsengleichung bekommen haben:
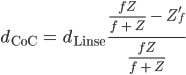
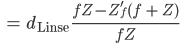
Jetzt benutzen wir den Ausdruck für aus der Linsengleichung:
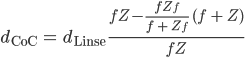
Nach ein paar elementaren Umformungen erhälst Du
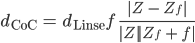
Max Okay, jetzt hast Du eine Gleichung , wo nur noch die Brennweite, der Abstand und der Fokusabstand sowie der tatsächliche Linsendurchmesser vorkommen.
Rike Stimmt. Den Linsendurchmesser berechnet man aus der Brennweite 
und der Blendenzahl 
:
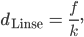
das ergibt
Die finale Formel für den CoC
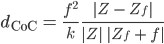
Max Hey, ist ja toll.
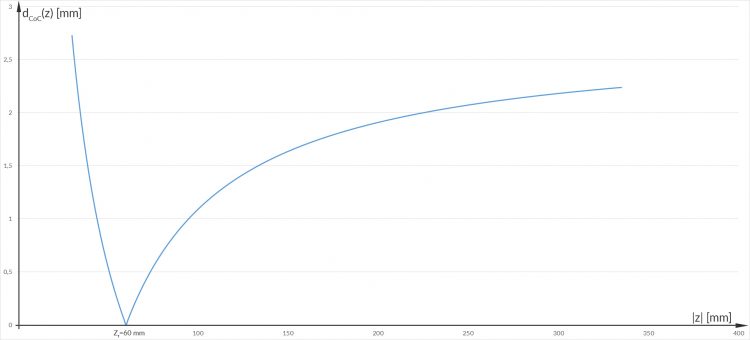
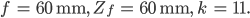Bei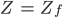 
ist der Circle of Confusion 0, weil da ja der Fokuspunkt ist, und der Punkt auf einen Punkt abgebildet wird.CoC für digitale Kameras
Rike Jetzt muss ich noch überlegen, wie die Kamera alles auflöst.
Max Das ist doch einfach, die kleinste Auflösung ist 1 Pixel. Bei der Nikon D800 haben wir dann
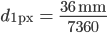
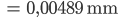
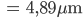
Und wenn der abgebildete Punkt mit dem Durchmesser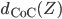 
kleiner als 1 Pixel ist:
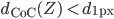
dann wird alles scharf abgebildet.
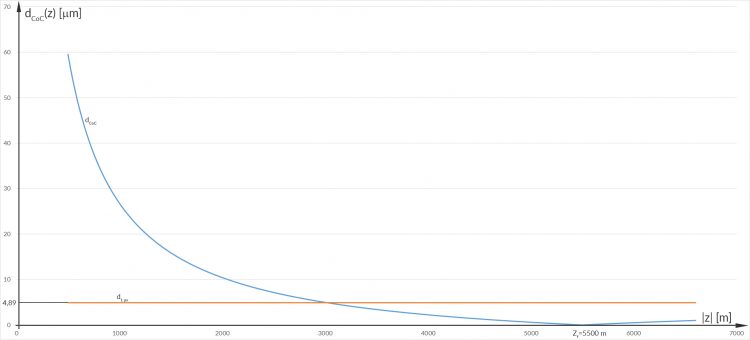
Rike Für
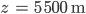
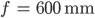
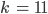
kriege ich mit dieser Formel alles scharf von 3 020 m bis Unendlich!
Max Jetzt mach mal ein Foto! Dein Objektiv war ja ziemlich teuer, das kann da wohl mithalten und bei der Blendenzahl hast Du auch noch keine Beugung an der Blende.
***
Übungsaufgaben
- Berechne den Grenzwert
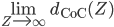
- Berechne für die Hyperfokale
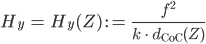
den Grenzwert
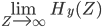
(Die Hyperfokale ist die Entfernung, bei der alles “scharf” abgebildet wird, wenn man auf den “unendlich fernen” Horizont fokussiert.)
- Was ergibt das für Rikes Setting?
Lösungen
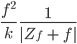
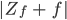
- ca. 5 500 m