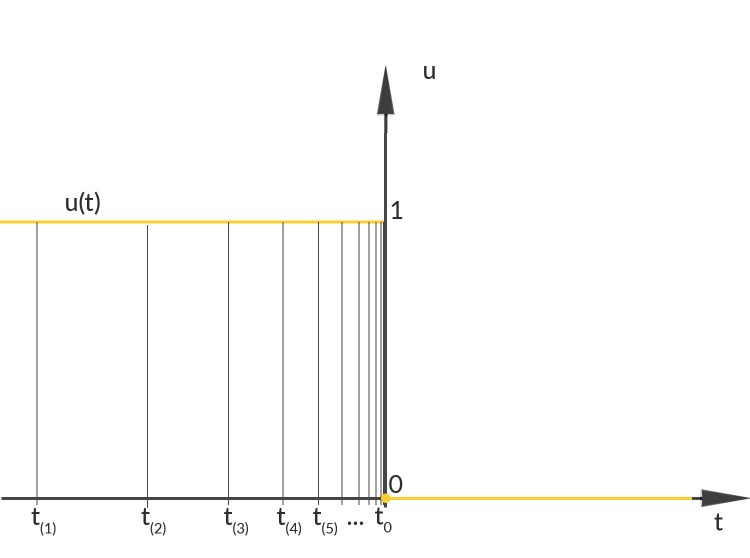
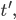Was ist mit unserem Zeitempfinden geschehen, wie gelingt es Nolan, 3 verschiedene Timelines: eine Woche „Mole“, einen Tag „Sea“ und eine Stunde „Air“ mit „einem kontinuierlichen Gefühl der Intensität“ zu vereinigen, und das „mit wachsender Intensität“? Ist das mathematisch ausdrückbar? Welche Art von Abbildungen haben wir vom „echten“ Geschehen zum Film?
Skalierung der Zeit
Zunächst skalieren wir alle Zeitleisten auf das Intervall 
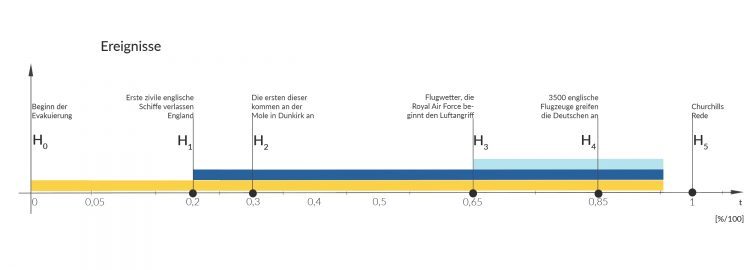
Funktionen 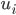
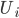
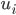
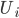
So können wir sinnvoll die folgenden Funktionen definieren:

ist die Funktion, die einem Zeitpunkt 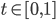
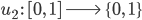
für die „Sea“ und
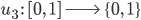
für die „Air“. Weiter ist
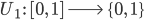
ist die Funktion, die einem Zeitpunkt 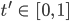
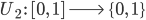
für „Sea“-Ereignisse im Film und
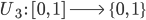
für „Air“-Ereignisse im Film. Alle diese Funktionen sollen den Raum 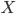
Eigenschaften von 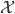
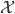
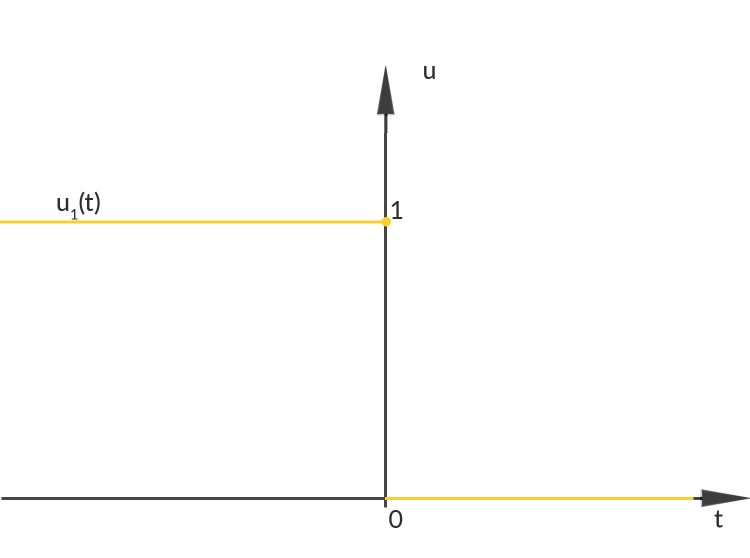
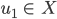
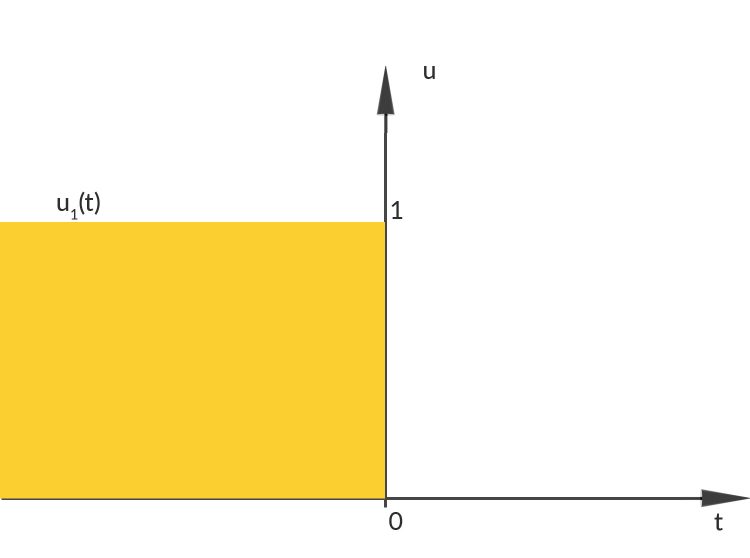
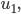
Offensichtlich sind die Funktionen an den Stellen, wo sie von 0 auf 1 oder umgekehrt springen, nicht stetig, denn dann ist für einen Punkt 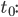
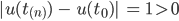
für geeignete

Konvergenz in 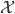
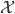
Die Funktionen 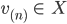
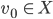

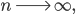
falls
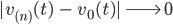
für 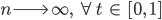
ist. Das ist die punktweise Konvergenz für Funktionen.
Zeittransformationen
Die Zeittransformationen 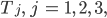
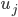
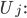

mit den Eigenschaften: Für jedes 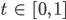

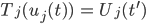
Solche Transformationen 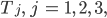
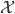
Außerdem gibt es weitere Forderungen:
1. Ordnungsrelation
Die Zeittransformationen 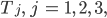
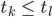
mit
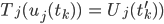
und
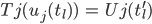
stets
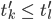
gilt.
2. Historische Referenzpunkte
Ferner sollen die Zeittransformationen 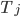
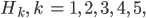
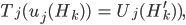
mit 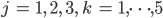
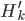
3. Gleichzeitigkeit
Und als letztes sollen die Überschneidungen der Timelines, die Interaktivitäten der Handlungen (fiktionaler Charaktere) beschreiben und eine Gleichzeitigkeit der Ereignisse im „echten“ Leben ermöglichen.
Für alle gleichzeitigen Ereignisse 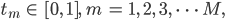
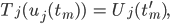
mit 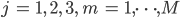
sein.
4. Topologie in 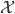
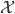
Wir sagen, die Transformationen 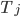
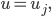
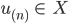

(siehe oben, Topologie in 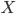
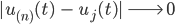
für

) stets
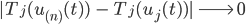
für

gilt. Das kann man ebenfalls punktweise Konvergenz nennen.
Ist es nun möglich, solche Zeittransformationen 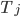
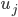
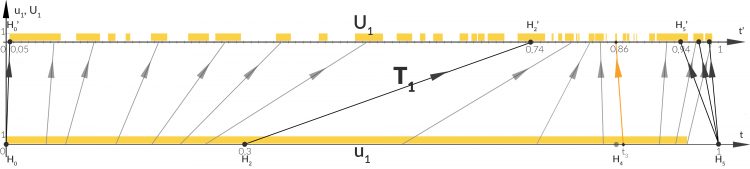
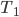 soll die Zeittransformation auf der „Mole“ beschreiben.
soll die Zeittransformation auf der „Mole“ beschreiben. 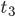 ist der Zeitpunkt, an dem Tommy auf die Yacht gerettet wird. Die Churchill-Rede (H5) wird hier vereinfachend als Punkt gezeichnet, sie war 12 Minuten lang. Da sich am Ende aufgrund der vorgezogenen Churchill-Rede die „Feldlinien“ schneiden, haben wir keine Beibehaltung der Ordnung. Spätere Augenblicke werden hier – relativ an anderen Ereignissen gemessen – früher gezeigt. Im Film war es möglich, zu einer Zeit gleichzeitig Ereignisse der Mole zu sehen, wie auch die Churchill-Rede zu hören und deren Motive an der Mole zu entdecken.
ist der Zeitpunkt, an dem Tommy auf die Yacht gerettet wird. Die Churchill-Rede (H5) wird hier vereinfachend als Punkt gezeichnet, sie war 12 Minuten lang. Da sich am Ende aufgrund der vorgezogenen Churchill-Rede die „Feldlinien“ schneiden, haben wir keine Beibehaltung der Ordnung. Spätere Augenblicke werden hier – relativ an anderen Ereignissen gemessen – früher gezeigt. Im Film war es möglich, zu einer Zeit gleichzeitig Ereignisse der Mole zu sehen, wie auch die Churchill-Rede zu hören und deren Motive an der Mole zu entdecken.

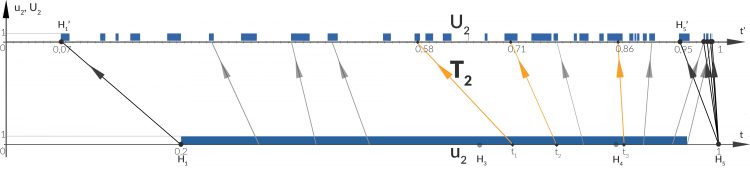
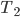 soll die Zeittransformation auf der Yacht, der „Sea“ beschreiben.
soll die Zeittransformation auf der Yacht, der „Sea“ beschreiben. 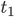 ist der Zeitpunkt der 1. Interaktion, wo die 3 Spitfire im Bild mit der Yacht zu sehen sind, bei
ist der Zeitpunkt der 1. Interaktion, wo die 3 Spitfire im Bild mit der Yacht zu sehen sind, bei 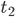 wird der Spitfire-Pilot Collins auf die Yacht gerettet,
wird der Spitfire-Pilot Collins auf die Yacht gerettet, 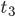 ist wie bei Abb. 2.
ist wie bei Abb. 2.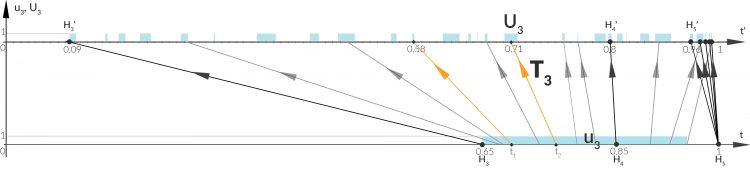
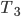 soll die Zeittransformation in der „Air“ beschreiben.
soll die Zeittransformation in der „Air“ beschreiben. 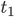 und
und 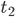 sind wie in Abb. 2 und 3.
sind wie in Abb. 2 und 3.Fazit
Offensichtlich lassen sich solche Zeittransformationen 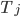
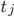
[Wird fortgesetzt]
***
Übungsaufgaben
- Konstruiere Zeittransformationen
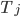 !
! - Was ändert sich, wenn die Zeiten