Urlaub mit komplexen Zahlen

Rike und Ben sind für ein paar Tage im Süden, Rike musste sich unbedingt erholen und etwas Sonne genießen, meinte Ben.

Ben Wieso kennst Du Dich eigentlich so gut mit Mathe aus, wo Du doch Medienproduktion studiert hast?

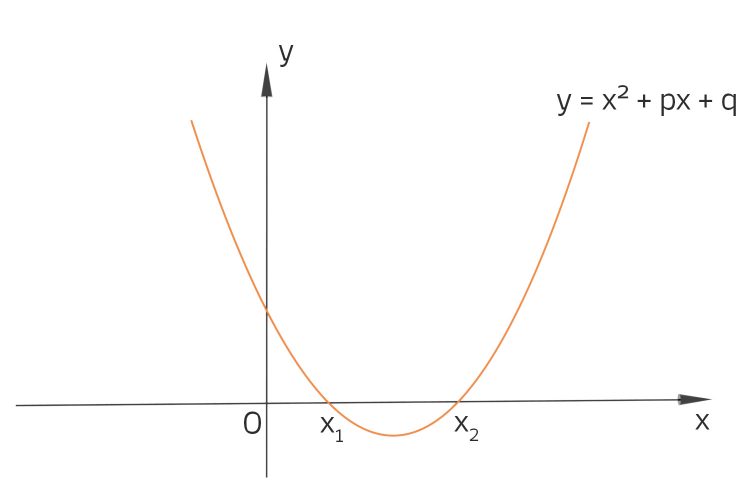
Rike Ach, weißt Du, als Kind habe ich ganz gern Mathe gemacht. Doch dann kam der Augenblick in der Schule, wo wir Parabeln, also solche

gezeichnet haben.

p-q-Formel im Reellen

Dann haben wir die Nullstellen bestimmt, also die quadratische Gleichungen in Normalform

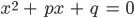
gelöst. Das habe ich mir im Mathelehrbuch angesehen. Ich habe die p-q-Formel zur Lösung der Nullstellen

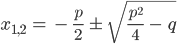
gefunden. Die klappt aber nur, wenn der Term unter dem Wurzelzeichen, die Diskriminante nicht negativ ist,

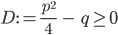
Dann schneidet die Parabel die x-Achse in x₁ und x₂.

Ben Klar.

p-q-Formel für komplexe Nullstellen

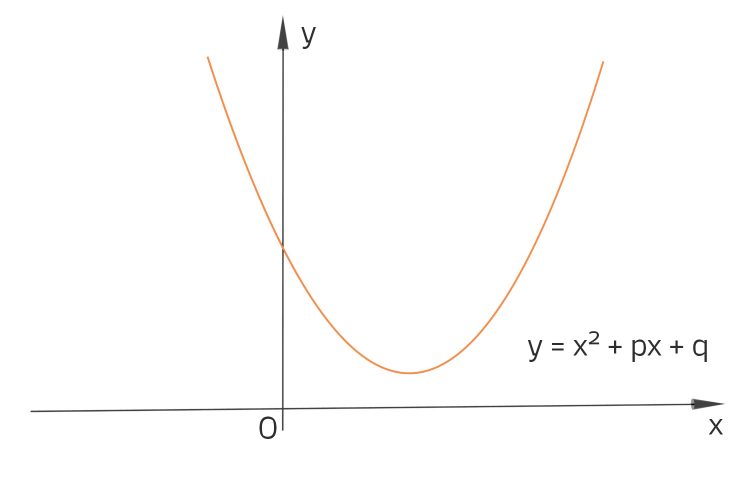
Rike Für den Fall, dass die Diskriminante kleiner Null ist, gab es im Lehrbuch keine Lösung. Das hat mich richtig wütend gemacht, der Lehrer hat mir auch nicht weitergeholfen. Da habe ich meine Mutter gefragt, Internet gab‘s damals noch nicht für mich, meine Mutter hat mir die komplexen Zahlen erklärt. Also, die p-q-Formel funktioniert dann immer noch, nur hast Du dann komplexe Zahlen, und Du kriegst die imaginäre Einheit i dazu:

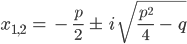
Da habe ich mir überlegt, dass die Parabeln die x-Achse nicht schneiden, jedenfalls nicht im Reellen. Das sieht so aus:

Ben Klar.

Eulerformel

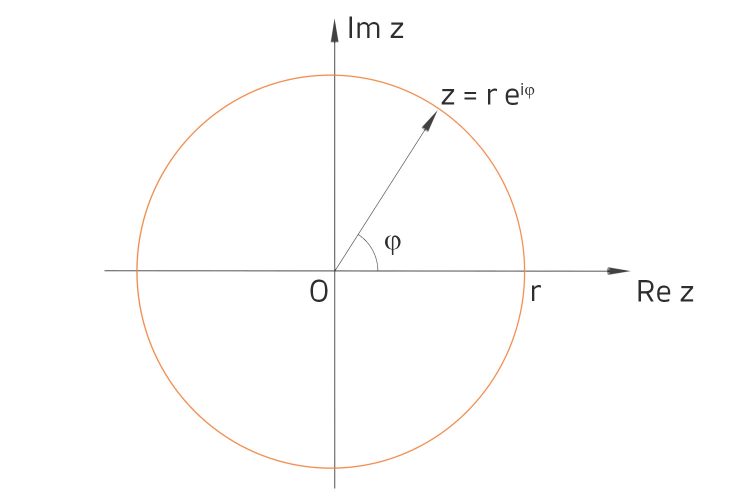
Rike Dann kennst Du ja auch die Eulerformel für komplexen Zahlen:

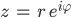
Ben Oh, ja, na klar. Man traut sich schon gar nicht mehr, sie schön zu nennen.

Komplexe Funktionen

Rike Haha, sie ist doch schön! Die Bezeichnungen und die Exponentialfunktion sind einfach genial. Wenn ich versuche, komplexe Funktionen

zu zeichnen, wird es schwierig. Die komplexen Zahlen haben zwei reelle Dimensionen, und als Abbildung kommt wieder eine komplexe Zahl raus, da brauchst Du den 4-dimensionalen Raum!

Ben Haha!

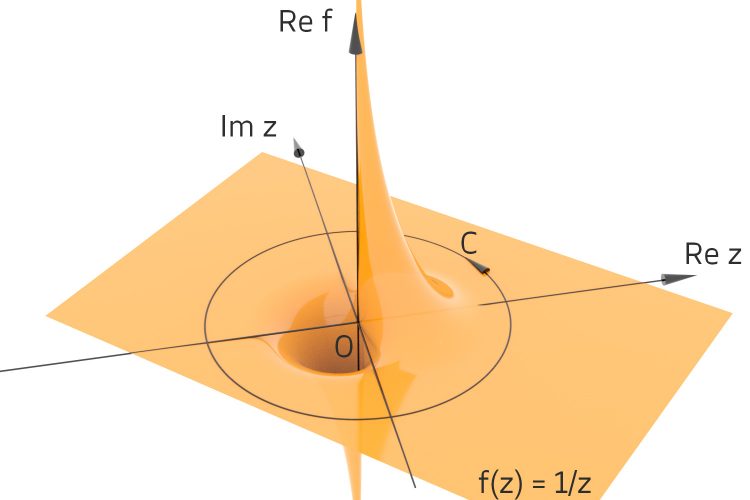
Rike Aber es gibt wunderbare Phänomene. Die habe ich in einem Buch gefunden, das hat mich gewissermaßen für den langweiligen Matheunterricht entschädigt. Wenn Du zum Beispiel die ganz einfache Funktion

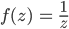
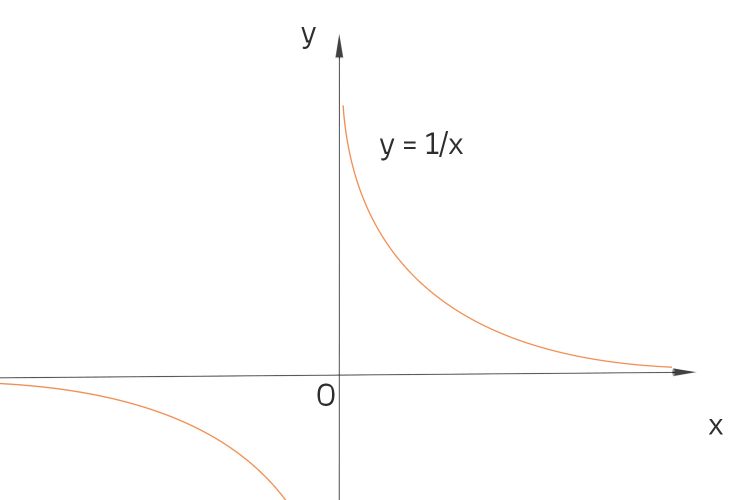
im Komplexen betrachtest, dann hat die - wie die reelle Funktion auch - in Null eine Polstelle.

Residuum

Im Komplexen kannst Du um die Nullstelle herumgehen, Du bist ja da in der Ebene und nicht wie im Reellen auf der x-Achse. Wenn Du auf diesem Weg um Null herum alle Werte der Funktion f(z) = 1/z integrierst, so:

Und dann die Eulerformel einsetzt

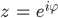
mit

und

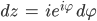
kriegst Du folgendes heraus:

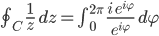
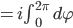
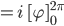
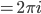
Ben Iss‘ ja krass!

Rike Nicht schlecht! Finde ich auch. Dieses Integral wird zum Klassifizieren von Funktionen und deren Polstellen benutzt. Die Zahl

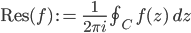
heißt Residuum. Dann habe ich für ein paar komplexe Funktionen das Residuum berechnet, das war wunderbar. Dann bin ich zweimal um die Polstellen herum gegangen, linksherum oder rechtsherum, wie Schlittschuhlaufen hat sich das angefühlt, als hätten die Funktionen und ihre Polstellen eine Seele.

Ben Rike, hört sich gut an. Vielleicht könnte man das Residuum benutzen, um Richtungen auf Kurven und Normalenrichtungen von Ebenen numerisch festzulegen?

Rike Ja, gute Idee, wollen wir das gleich mal programmieren?

***

Übungsaufgaben

Berechne das Integral für einen Kreis um i mit dem Radius ½!

Lösung

0